선형회귀(LinearRegression)는 선형함수를 이용하여 회귀를 수행하는 방법이다.
회귀(回歸, 영어: regress )의 원래 의미는 옛날 상태로 돌아가는 것을 의미한다. 영국의 유전학자 프랜시스 골턴은 부모의 키와 아이들의 키 사이의 연관 관계를 연구하면서 부모와 자녀의 키사이에는 선형적인 관계가 있고 키가 커지거나 작아지는 것보다는 전체 키 평균으로 돌아가려는 경향이 있다는 가설을 세웠으며 이를 분석하는 방법을 "회귀분석"이라고 하였다. (https://ko.wikipedia.org/wiki/회귀_분석)
선형 회귀(線型回歸, 영어: linear regression)는 종속 변수 y와 한 개 이상의 독립 변수 (또는 설명 변수) X와의 선형 상관 관계를 모델링하는 회귀분석 기법이다. (https://ko.wikipedia.org/wiki/선형_회귀)
선형회귀의 방법은
- 학습하고자하는 가설을 수학적인 표현식으로 나타내고
- 가설의 성능을 측정할수 있는 손실함수를 정의한 다음
- 손실함수를 최소화 할수 있는 알고리즘을 작성하게 된다.
[1] 먼저 필요한 라이브러리를 설치한 뒤 다음과 같이 import 를 한다.
import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
[2] 가설을 정의하는 방식을 Pytorch에서는 다음과 같은 코드를 사용한다. nn.Linear의 두 변수는 입력되는 차원의 갯수와 출력되는 차원의 갯수를 의미한다. 예를 들어 다음과 같이 1, 1을 입력하게 되면, 2차원 그래프의 x, y값이 입력되는 것으로 보면 된다.
# 선형회귀 모델을 지정한다.
model = nn.Linear( 1, 1 ) # input_size, output_size
[3] 입력과 출력에서 훈련 데이터로 사용될 데이터 셋을 준비한다.
# 데이터셋 준비
x_train = np.array([[1],[2],[3],[4],[5]], dtype=np.float32)
y_train = np.array([[3],[6],[9],[12],[15]], dtype=np.float32)
test_data = np.array([[6]], dtype=np.float32)
[4] 손실함수와 옵티마이저를 정의한다. 손실함수(또는 비용함수)는 가설로 만들어진 선형모델(nn.Linear)에 훈련데이터를 대입했을 때의 차이를 계산하는 함수인데, 대표적인 손실함수 중 하나인 평규제곱오차(MSE: Mean of Squared Error)을 사용한다. 옵티마이저는 손실함수가 최소화되는 방향으로 선형모델을 조정하는 역할을 하는데 경사하강법(Gradient Descent)기법을 사용한다. lr(learning_rate) 변수는 한번 학습을 할때마다 x값의 이동 값이 된다.
# 손실함수와 옵티마이저 정의
criterion = nn.MSELoss() #MSE 손실함수
optimizer = torch.optim.SGD(model.parameters(), lr=0.001) # 경사하강법
[5] 위에서 정의된 함수들과 변수를 이용해서 다음과 같이 실제 학습(트레이닝)을 진행할 수 있다.
# numpy array에서 torch tensor 변경
inputs = torch.from_numpy(x_train)
targets = torch.from_numpy(y_train)
num_epochs = 500 # 훈련할 총 횟수
# 트레이닝
for epoch in range(num_epochs):
# forward 연산
outputs = model(inputs)
loss = criterion(outputs, targets)
# backword 연산
optimizer.zero_grad() # 이전에 계산한 값을 초기화
loss.backward()
optimizer.step() # 손실이 적은 step으로 변경
if (epoch+1) % 5 == 0: # 훈련횟수를 5번 수행한 시점에 상태 출력
print (f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')
[6] 500번 훈련을 수행한 모델의 출력결과를 실제 데이터와 비교하는 그래프를 만들어 본다.
# 예측 결과 시각화
predicted = model(torch.from_numpy(x_train)).detach().numpy()
plt.plot(x_train, y_train, 'ro', label='Original data')
plt.plot(x_train, predicted, label='Fitted line')
plt.legend()
plt.show()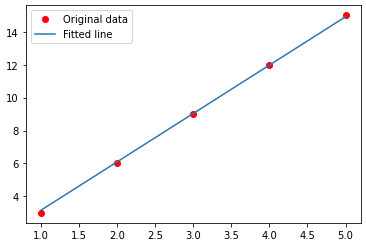
[7] test_data의 값 6에 대한 예측값을 모델에 입력하여 출력해 볼 수 있다. 다음 코드를 실행해보니 예측한 y값이 17.843039 로 출력되었다. 약간에 오차가 있지만 크지 않았다.
y_pred = model(torch.from_numpy(test_data)).detach().numpy()
print(f'예측한 y값 : {y_pred}')
주어진 테스트 데이터를 학습하여 최적의 선형함수 모델을 만들어내는 과정이 신기해 보였다. 실제 수학적이 내용을 이해하기는 쉽지 않았지만 선형회귀를 이용한 개념을 이해할 수 있었다.
'Programming > Python' 카테고리의 다른 글
| Flask 웹사이트 구축 - 5. 웹페이지(html) 렌더링을 하는 뷰 함수들 (0) | 2022.06.27 |
|---|---|
| Flask 웹사이트 구축 - 4. 데이터베이스 연결하기 (0) | 2022.06.25 |
| Flask 웹사이트 구축 - 3. 메인 웹어플리케이션 생성 (0) | 2022.06.21 |
| Flask 웹사이트 구축 - 2. 개발방향과 데이터베이스(sqlite3) (0) | 2022.06.21 |
| Flask 웹사이트 구축 - 1. 개발환경 goormIDE 준비 (0) | 2022.06.20 |